BESPOKE TALK Series: BESO a New Paradigm for Optimizing Structures
- John Michael Jalandra

- Nov 14, 2022
- 7 min read
Updated: May 30, 2023
BESO - Bi-Directional Evolutionary Structural Optimization / Structural Topology Optimization.
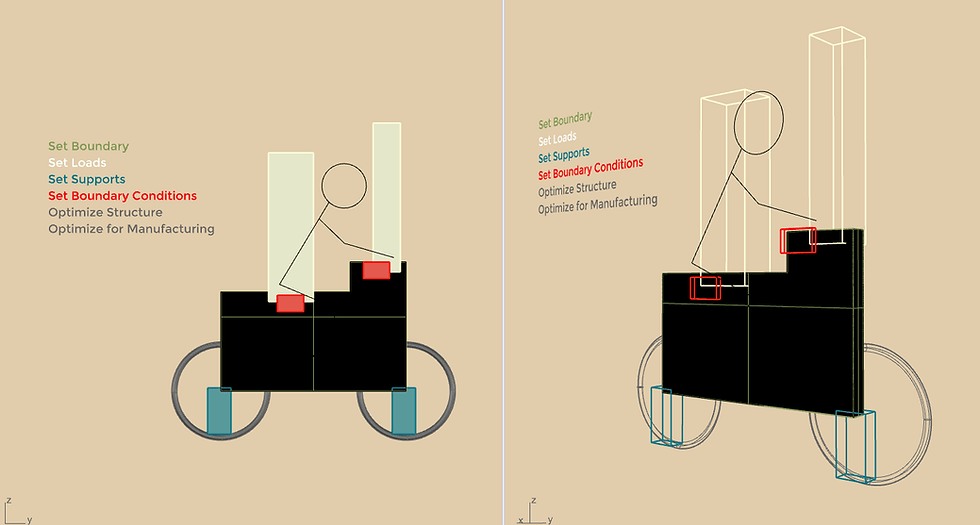
ESO and BESO
The ESO approach is based on the idea of evolution, in which a population of structures is subjected to a succession of selection and mutation operators. The best-performing structures are chosen for reproduction, and their children are altered. The method is repeated until the population has reached the globally optimal solution.
The BESO method is a modification of the ESO method that allows for simultaneous material insertion and removal. This allows you to start with any basic design and expand the structure to its full potential. The ESO and BESO methods are effective structural optimization tools. They are based on the idea of evolution, in which a population of structures is subjected to a succession of selection and mutation operators. The best-performing structures are chosen for reproduction, and their children are altered. The method is repeated until the population has reached the globally optimal solution.
Topology Optimization
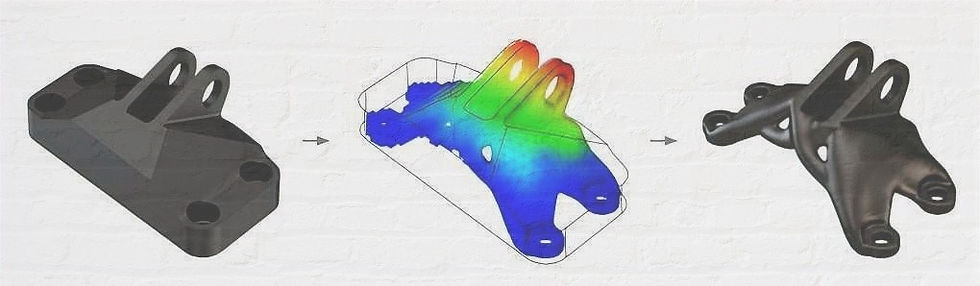
Typical TO design steps (source: engineering.com)
Definition: A method for optimizing the structure and arrangement of materials inside a predetermined three-dimensional geometrical design space according to the designer's own standards.
Goal: Mathematical modeling and optimization of characteristics including environmental forces, load conditions, boundary conditions, restrictions, and material quality are employed to achieve this goal.
How it works:
The designer begins by determining the smallest allowable design space for the component.
When the user specifies the loads, constraints, and material properties from the outside world.
After that, FEA takes into account the smallest possible geometric design envelope and partitions the design space accordingly.
TO uses finite elements to generate a simple mesh in the constrained design space. The optimum load or stress that an element can withstand is then determined by analyzing the mesh's stress distribution and strain energy.
The TO software then checks the code for bugs and removes any unnecessary parts.
The software then compares the values of each finite element's stiffness, compliance, stress, and deflection to the requirements you've set up in order to identify any unnecessary components.
The pattern is finished with a last stitch: finite element analysis.
Advantage | Disadvantage |
|
|
TO Advantages
Optimized design – FEA takes numerous elements into account and prevents making risky assumptions that could result in a defective design.
Minimize material – the capacity to eliminate unneeded material while increasing the stiffness-to-weight ratio. Smaller items and lower energy use arise from reduced weight and size. Furthermore, the improved design will save raw materials.
Cost-effective – a quality system procedure. Because you are placing material only where it is required, you are using less material and spending less money. Additionally, it uses less energy to move and transport and less packing. Many of the intricate geometries produced by topology optimization would make it impossible to manufacture them using conventional methods. However, this complexity incurs no additional costs when paired with 3D printing.
Environmental impact reduction – it generates less waste. However, if the inappropriate manufacturing is chosen, this might not be the case. For instance, plans for topology optimization are more suited for additive manufacturing. It's crucial to start the design model as tiny as feasible for subtractive manufacturing in order to reduce material removal and waste.
Faster iterative design process – running through several modes and considering the straining of the components minimizes the likelihood of failure.
TO Disadvantages
Manufacturing constraints, Costlier - because some of the best designs are only suitable for 3D printing, injection molding, or die casting. However, as compared to some traditional production methods, the cost of additive manufacturing remains high.
Lack of understanding – even while topology optimization has been around for a while, it is only now, with the advent of AM, that it is becoming more prominent. Although new tools are being offered, they still need time to develop and support the sector.
Principal Stress Lines
What is principal stress-lines? Simply put, they are orthogonal curve pairs that represent internal force trajectories. In other words, they idealize material continuity paths and naturally encode the optimal topology for any structure given a set of boundary conditions.
Why are principal stress-lines important? First and foremost, they provide a theoretical framework for understanding how force is transmitted through a material. This understanding is critical for designing structures that are both safe and efficient. In addition, principal stress-lines can be used to predict the behavior of a structure under different loading conditions. This is extremely useful for engineers, as it allows them to plan for potential problems before they occur. Finally, principal stress-lines can be used to optimize the topology of a structure. By understanding how force is transmitted through a material, engineers can design structures that use less material while still providing the same level of support. This is important not only for economic reasons, but also for environmental reasons.
Marching Cube Algorithm

Marching Cube Algorithm for Implicit surface plotting (source: shamshad-npti.github.io)
The Marching Cube Algorithm is a method for generating straight and curved isosurfaces using volume data. This technique is utilized in many different industries, including medical imaging and computer graphics.
The algorithm's core idea is to take a grid of points and determine whether the isosurface goes through each one. If this is the case, a triangle is formed to contain that point. This method is repeated for all grid points, yielding a set of triangles that approach the isosurface.
There are several ways to construct the Marching Cube Algorithm, but they all follow a similar procedure. The volume data is first discretized into a grid of points. The isosurface is then analyzed for each point on the grid to see if it passes through that place. If this is the case, a triangle is formed to contain that point. This method is repeated for all grid points, yielding a set of triangles that approach the isosurface.
The Marching Cube Algorithm is a fast method for extracting isosurfaces from volume data. It can make both straight and curved surfaces and is used for many things, such as computer graphics and medical imaging.
The Marching Cubes algorithm is also known as the following:
Given an object, a test to discover whether an arbitrary point is within the object as well as the bounds of the object is:
Divide the enclosed space into an arbitrary number of cubes. Check the corners of each cube to see if they are inside the object. The surface must traverse through every cube, where some corners are within and some are outside the item, intersecting the borders of the cube in between corners of opposing categorization. Draw a surface linking these crossings within each cube. You've got your target.
Key points
Iteration in topological optimization involves the removal of parts that are irrelevant in supporting the applied stress on the object
The final iteration is the best topology for supporting the applied load with the least "parts”
Deformation is small, stiffness is high.
tOpos vs Ameba vs Karamba3D
tOpos is a plugin for optimizing 3D topology that was built on the SIMP methodology
developed by Bendsoe and Sigmund. The iterative conjugate gradient method is employed while trying to solve problems using the BLAS. The user has the option of choosing between the MatrixFree version or the Preassembled version of the solver.

Topos 3D Flow (source: Food4Rhino)
Penalization approach on a solid isotropic material
The SIMP technique predicts an ideal material distribution within a certain design space for given load circumstances, boundary conditions, manufacturing constraints, and performance objectives.
The algorithm's core idea is to take a grid of points and determine whether the isosurface goes through each one. If this is the case, a triangle is formed to contain that point. This method is repeated for all grid points, yielding a set of triangles that approach the isosurface.
The border object in tOpos is discretized as voxels. It will examine the stress lines traveling through the voxels after applying the applied load and supporting it through a number of iterationsload and supporting it through a number of iterations. Each iteration, a penalty is assigned to the voxels through which no stress lines travel, eliminating them from the grid.
Black voxels indicate the voxel where material is required
White voxels indicate the voxels to be removed
The topology set by the black voxels on the final iteration is the most optimized

Ameba is an open-source topology optimization tool based on the BESO approach and the FEniCS computer platform. Depending on the design needs, the user may apply different loading and boundary conditions to the initial design domain. During the software's computational process, the design domain will expand into numerous shapes, akin to an ameba, and eventually reach an organic form that is structurally efficient.
Ameba (source: Food4Rhino)



Initial part geometry design – A portion frame or design space is created by the user.
Define preserved geometry areas – The user then specifies some key regions to maintain, such as mounting screw headspace and material around bearing bore diameter.
Define loads, constraints, and material – At this point, the user applies loads and constraints. The material and properties of the part are also assigned.
Mesh generation and remeshing – Mesh delineation and refinement is a crucial part of topology optimization.
Pick an optimization goal - Determine what you want to achieve.
Optimizing the run-topology – A program takes control and examines the component to
Analyze the results - Analyze the results but alter the levels to find the crucial regions that FEA highlighted.

Karamba3D is a finite element (FE) program for predicting the behavior of structures under external loads.
Finite Element Method: A general numerical method used to solve partial differential equations. The FEM subdivides a large system into smaller, simpler parts that are called finite elements. Simple equations model these finite elements which are then assembled into a larger system of equations that models the entire problem. The FEM then approximates a solution by minimizing an associated error function via the calculus of variations. Karamba3D (source: Food4Rhino)
BESO for Beams

Initially, a triangular mesh is formed from a surface, which is seen on the left. Both horizontal and vertical loads can be applied to a building in the same plane, but they are treated differently. Only three of the structure's nodes at the corners are free to move. In the right image, you can see that after 20 rounds of optimization, the structure's mass was reduced from its starting point by 45%.
The BESO procedure discards a number of the structure's least stressed and, hence, least efficient parts. At a predetermined volume or when there are no more of the original structural elements to remove, this iterative process terminates.
Application
Aerospace – weight reduction
Automotive – parts that are light and strong enough to withstand tension and impact without breaking.
Architecture - uncommon structural typologies, material usage.
Conclusion
Through topology optimization, designers are able to
Explore nontraditional design and not be constrained by the rigidity that comes with traditional structural design
Gain a deeper understanding on how architectural and structural design correlate to each other
Save on material and quantity cost
Save time for structural design
Lessen threat for human error
Pia Marañon Hazel Jumawan Januarius Anthony Panes
Lead Researchers
John Michael Jalandra
Content Writer
BERSABARC Design Studio 2022


